Problemi del linguaggio geometrico
La matematica che studiamo ed utilizziamo oggi è il frutto del lavoro di tanti uomini e di tante idee; forse l’idea più feconda di conseguenze è stata l’invenzione del linguaggio simbolico che noi chiamiamo algebra, risalente al Rinascimento italiano, ma con radici nella tradizione araba. Tale linguaggio (universale) è costituito da un sistema di numeri e lettere che permette di esprimere in maniera sintetica, concreta e immediatamente fruibile quantità astratte e con esse sviluppare calcoli e generalizzare concetti.
Euclide non possedeva questo potente strumento, ma poteva far ricorso solo al linguaggio descrittivo di tipo geometrico, con il quale operava confronti tra segmenti e superfici per dimostrare la congruenza dei vari enti geometrici e l’equivalenza tra le superfici stesse.
Un altro strumento che Euclide non utilizzava e con cui invece noi siamo abituati a lavorare sono le nozioni metriche, cioè il considerare la misura delle grandezze attribuendo a ciascuna un valore numerico dopo averla confrontata con una grandezza omogenea presa come unità di misura. Con le nozioni metriche ovviamente due figure hanno la stessa superficie se ad esse si può attribuire lo stesso numero come misura. Euclide invece non avendo questo strumenti si appoggia a considerazioni legate a questioni di proporzionalità o di equiscomponibilità.
E’ quindi non sempre facile per noi che traduciamo ciò che scrivono Platone ed Euclide rendere in italiano concetti che siamo abituati ad esprimere (in modo più efficace e sintetico) con la simbologia algebrica.
Per esempio il teorema di Pitagora viene illustrato da Euclide nella proposizione 47 del libro I degli Elementi nel seguente modo:
Ἐν τοῖς ὀρθογωνίοις τριγώνοις τὸ ἀπὸ τῆς τὴν ὀρθὴν γωνίαν ὑποτεινούσης πλευρᾶς τετράγωνον ἴσον ἐστὶ τοῖς ἀπὸ τῶν τὴν ὀρθὴν γωνίαν περιεχουσῶν πλευρῶν τετραγώνοις.
Nei triangoli rettangoli il quadrato del lato che sta sotto all’angolo retto è uguale ai quadrati dei lati che circondano l’angolo retto
Con il linguaggio algebrico l’area di un quadrato di lato AB si
esprime semplicemente con un simbolo del tipo ![]() ed il teorema di Pitagora diventa l’identità
ed il teorema di Pitagora diventa l’identità
![]()
Ecco un altro esempio.
La regola del quadrato di un binomio viene scritta da Euclide nella proposizione 4 del libro II degli Elementi nel seguente modo:
Ἐὰν εὐθεῖα γραμμὴ τμηθῇ, ὡς ἔτυχεν, τὸ ἀπὸ τῆς ὅλης τετράγωνον ἴσον ἐστὶ τοῖς τε ἀπὸ τῶν τμημάτων τετραγώνοις καὶ τῷ δὶς ὑπὸ τῶν τμημάτων περιεχομένῳ ὀρθογωνίῳ.
Se viene divisa come capita una linea retta, il quadrato (costruito) da tutta (la retta) è uguale ai quadrati (costruiti) dalle parti e al doppio del rettangolo circondato dalle parti.
Il linguaggio algebrico permette di esprimere lo stesso concetto con la formula
![]()
Il metodo geometrico dimostra questa proprietà facendo una figura
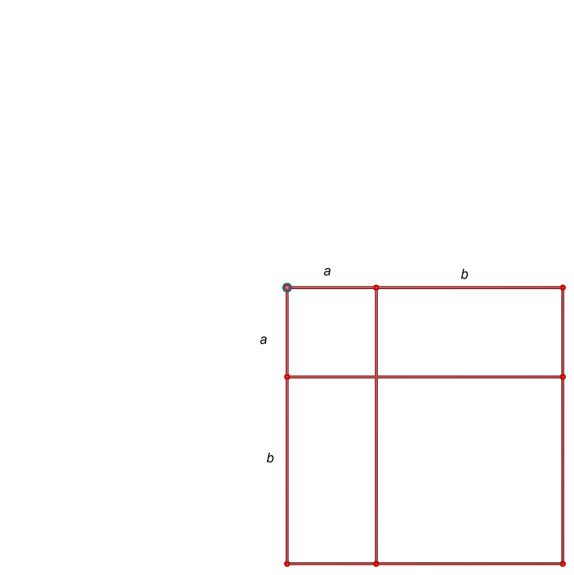
e dimostrando che il quadrato si scompone in due quadrati e due rettangoli.
Il metodo algebrico dimostra questa proprietà svolgendo i calcoli:
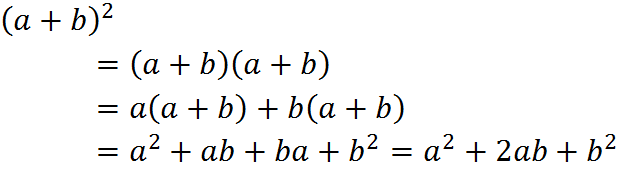
Proprio per queste ragioni, nel lavoro dello scorso anno sull’icosaedro, abbiamo dovuto inserire nella traduzione del testo di Euclide le “note del traduttore”: dopo aver interpretato il pensiero di Euclide a partire da una resa aderente più possibile al testo originale, lo abbiamo transcodificato nel nostro linguaggio matematico corrente per permettere la fruibilità del testo stesso.