Domanda 5 a)

Consideriamo tre punti A, B e C non allineati.

Quante sono le circonferenze passanti per essi?

Dove si trovano i loro centri?

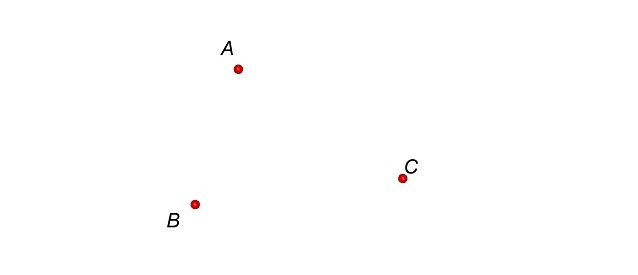
Cerchiamo innanzitutto le circonferenze passanti per A e B.

Abbiamo appena visto che i centri di queste circonferenze stanno sull’asse del segmento AB.

Cerchiamo ora le circonferenze passanti A e C.

Sappiamo che i loro centri stanno sull’asse del segmento AC.

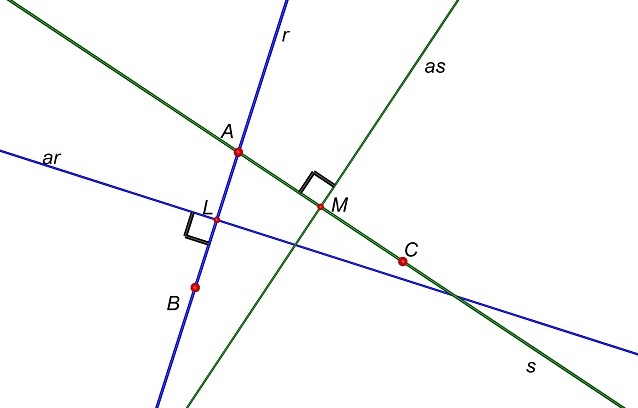
Ma allora le circonferenze passanti per A, B e C devono avere il centro sia sull’asse del segmento AB che sull’asse del segmento AC. Ma allora i centri devono stare nel punto di intersezione P dei due assi.

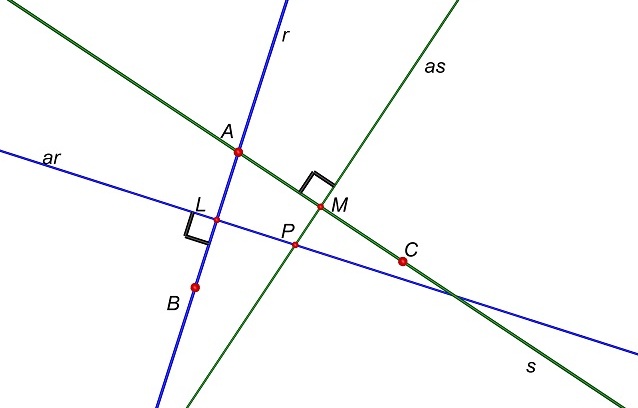
Osserviamo che, poiché il punto P appartiene all’asse del segmento AB, si ha:

d(P,A) = d(P,B)

(dove con d(P,A) indichiamo la distanza tra P e A).

Analogamente, poiché il punto P appartiene all’asse del segmento AC, si ha:

d(P,A) = d(P,C)

Ma allora da queste due uguaglianze segue:

d(P,A) = d(P,B)

e quindi il punto P appartiene all’asse del segmento AB.

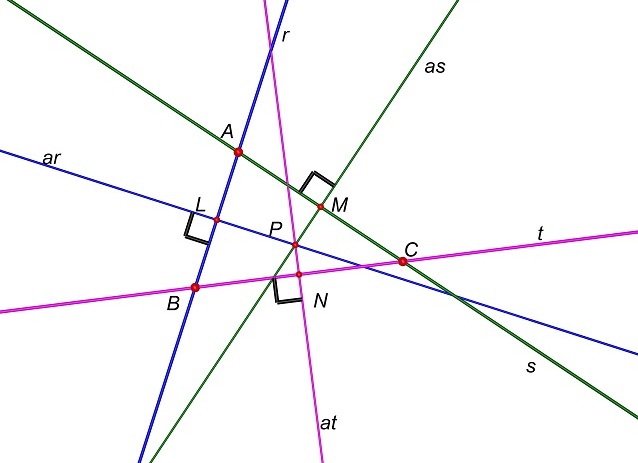
Abbiamo pertanto dimostrato un importante teorema.

Teorema.

Gli assi dei lati di un triangolo hanno un punto di intersezione.

La circonferenza di centro P passante per A passa anche per B e C.

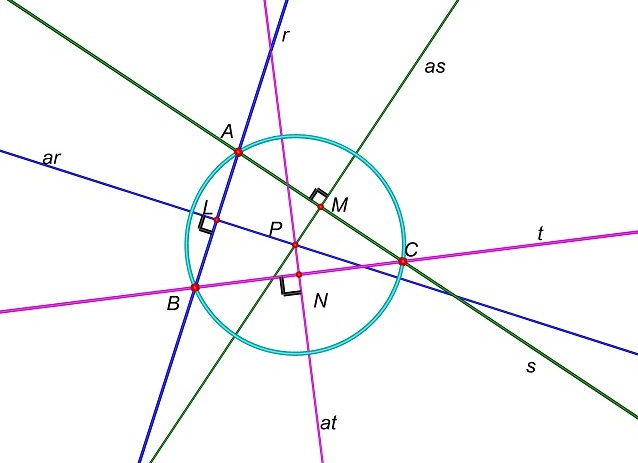
Abbiamo pertanto risposto alla nostra domanda.

Dati tre punti non allineati A, B e C, esiste una ed una sola circonferenza passante per essi. Il suo centro si trova nell’intersezione degli assi del triangolo ABC.

Domanda 4 b)

Consideriamo tre punti A, B e C.

Quante sono le sfere passanti per A, B e C?

Dove si trovano i loro centri?

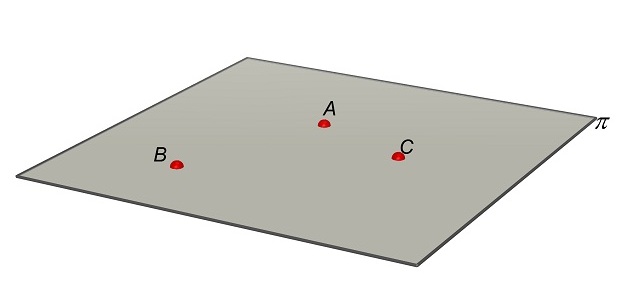
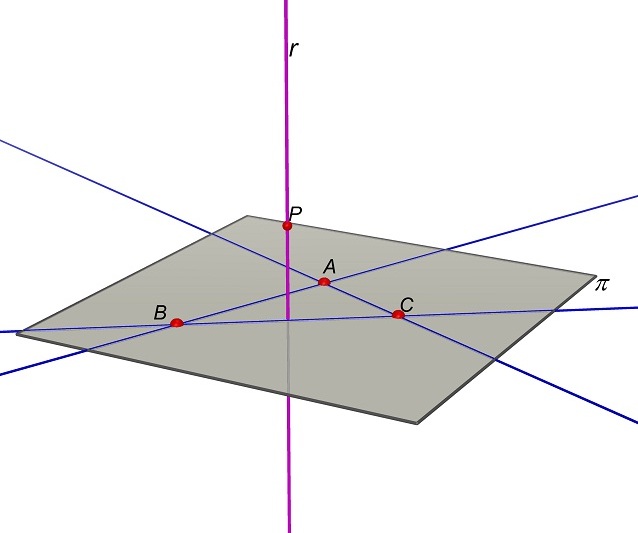
Nella figura abbiamo indicato il piano π passante per A, B e C.

Per rispondere alle domande usiamo un metodo analogo a quello usato per rispondere alla domanda precedente.

Cerchiamo innanzitutto le sfere passanti per B e C.

Abbiamo visto nella risposta alla domanda 4a) che i centri di queste sfere stanno sul piano asse α del segmento BC.

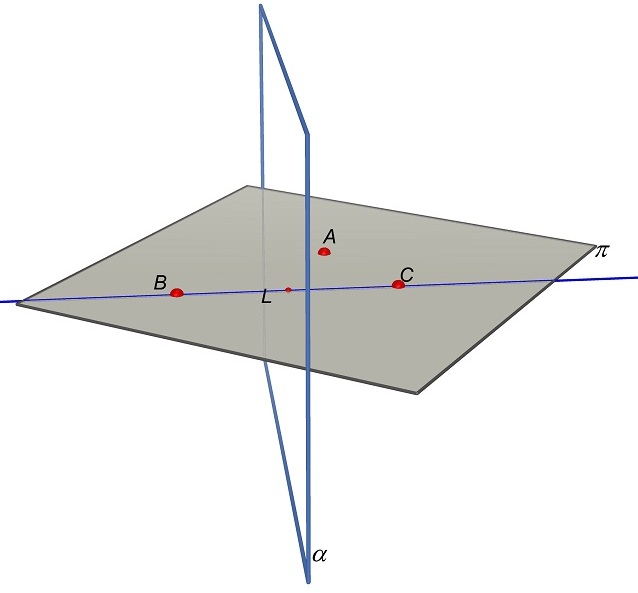
Cerchiamo ora le sfere passanti A e C.

Sappiamo che i loro centri stanno sul piano asse β del segmento AC.

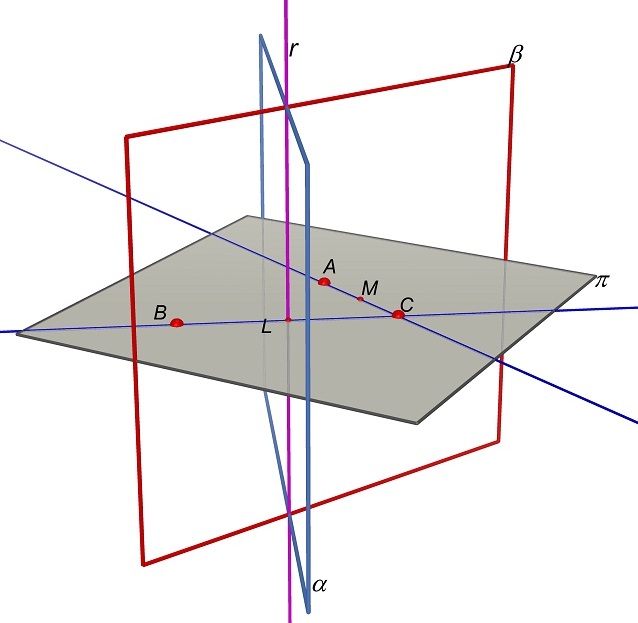
Ma allora le sfere passanti per A, B e C devono avere il centro sia sul piano asse α del segmento BC che sul piano asse β del segmento AC. Ma allora i centri devono stare nella retta r intersezione dei piani α e β.

Consideriamo ora tutti i punti P appartenenti alla retta r, intersezione del piano α con il piano β.

Per ognuno di questi punti si ha:

d(P,B) = d(P,C) e

d(P,A) = d(P,C)

Ma allora da queste due uguaglianze segue:

d(P,A) = d(P,B)

e quindi il punto P appartiene al piano γ asse del segmento AB.

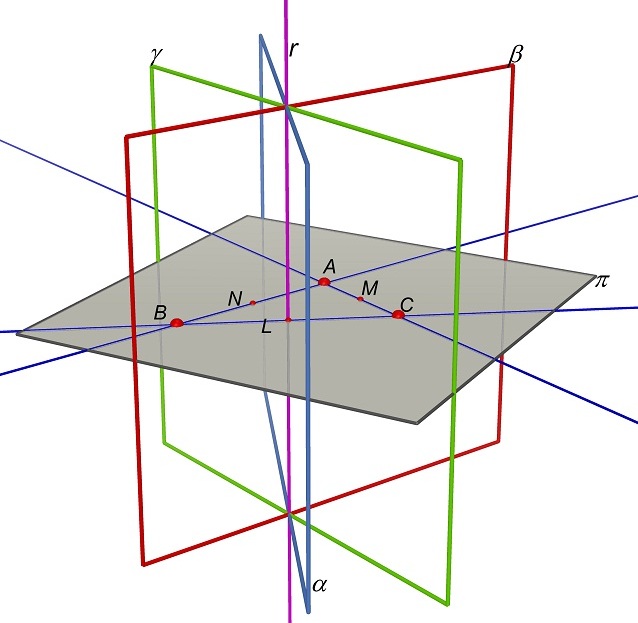
Se quindi consideriamo un qualsiasi punto P appartenente alla retta r intersezione dei piani assi dei segmenti BC, AC e BC:

Cliccando sulla figura si può muovere il punto P.

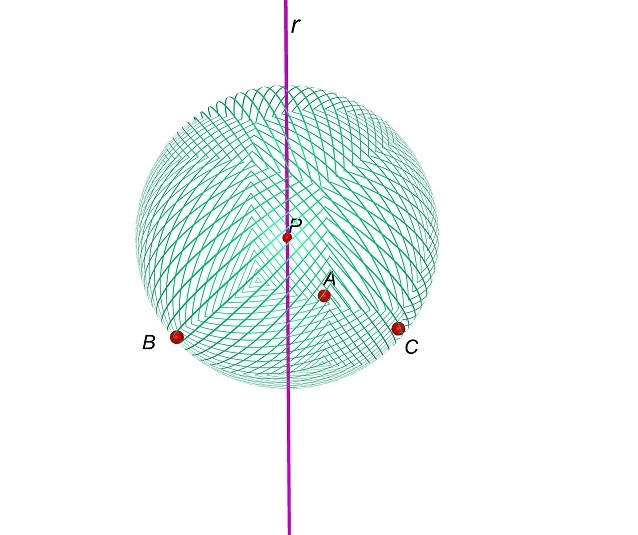
E consideriamo la sfera di centro P passante per A, otteniamo una sfera passante per A, B e C.

Cliccando sulla figura si può muovere il punto P.

Abbiamo pertanto risposto alla nostra domanda.

Dati tre punti non allineati A, B e C, esistono infinite sfere passanti per essi.

Il loro centri si trovano nella retta intersezione dei piani assi dei segmenti BC, AC e AB.

E’ interessante considerare, tra tutti i punti P della retta r, quello appartenente al piano π passante per A, B e C.

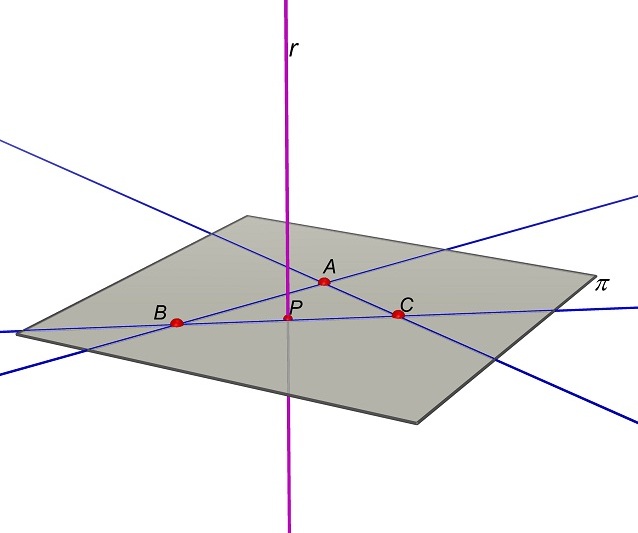
Consideriamo ora la sfera di centro P passante per A. Essa passa anche per B e C.

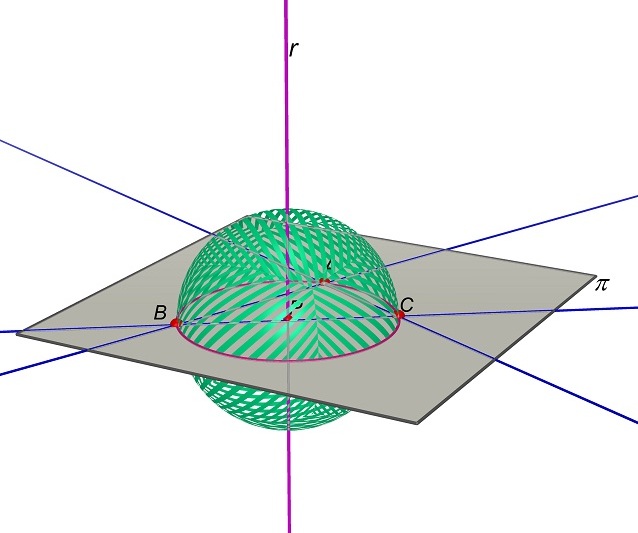
Sappiamo poi che per i punti A, B e C passa una sola circonferenza:

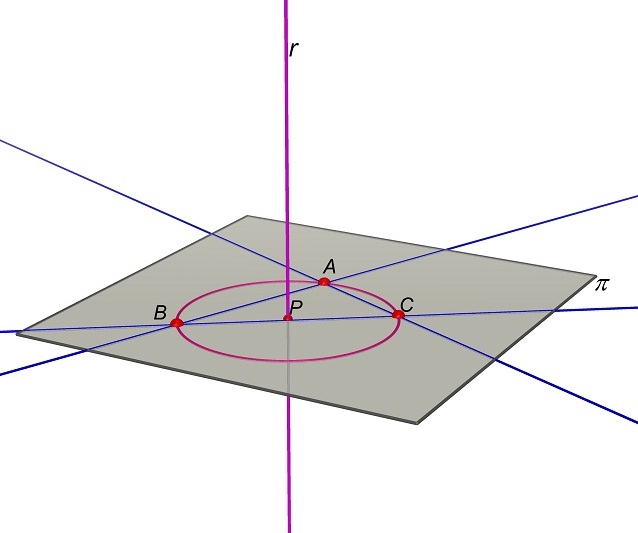
Che relazione c’è tra questa circonferenza e la sfera precedente?

Lasciamo la risposta al lettore.

Che relazione c’è tra la retta r e il piano π?

Lasciamo anche questa risposta al lettore.