Domanda

Con una livella è possibile controllare se un tavolo è orizzontale? Come? Perché?

Spunto preso da:

V. Villani Cominciamo dal punto

Pitagora Editrice, Bologna.

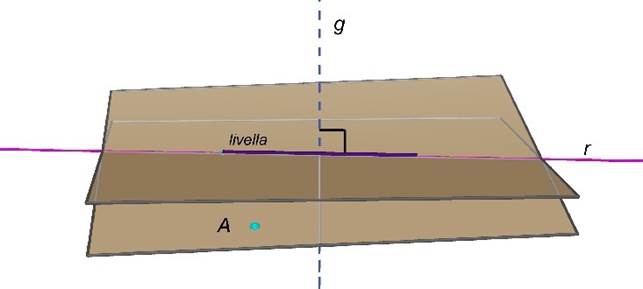
Come si usa una livella.

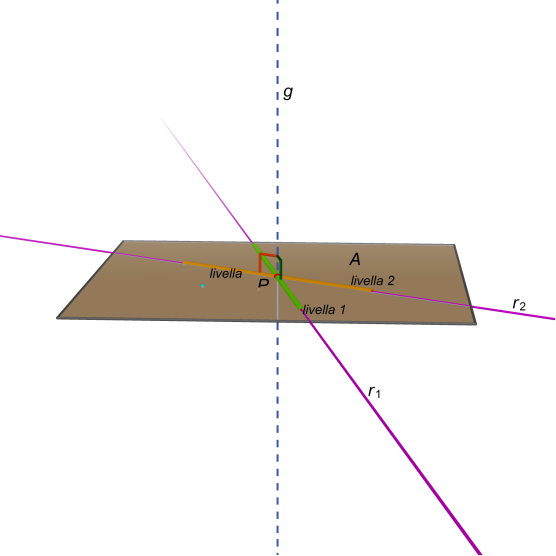
Poniamo la livella su un tavolo. Indichiamo con r la retta su cui abbiamo posto la livella.

Se la bolla d'aria della livella sta al centro, allora la retta r è perpendicolare alla retta g, corrispondente alla forza di gravità, passante per il centro della livella.

Poiché la retta g è ovviamente verticale, la retta r è orizzontale.

Verso la risposta

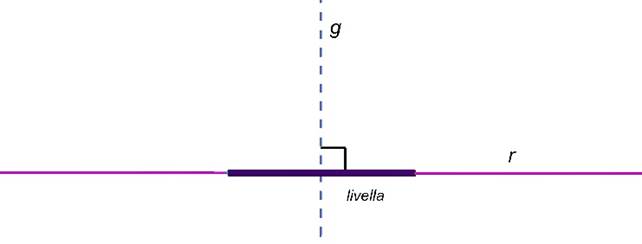
Poniamo la livella la livella sul tavolo e controlliamo che la bolla d'aria sia al centro.

Ma, facciamo attenzione, se la bolla sta al centro non è detto che il piano sia orizzontale.

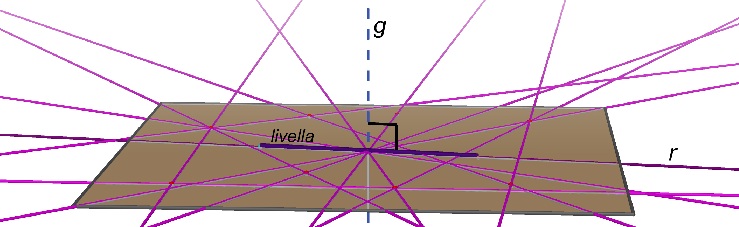
Infatti esistono infiniti piani contenenti la retta r: solo uno di essi è orizzontale.

Cliccando sulla figura puoi muovere il punto A e quindi ruotare un piano intorno alla retta r.

In effetti un tavolo è orizzontale se sono orizzontali tutte le rette del piano.

Quindi noi dovremmo fare infiniti controlli. Uno per ogni retta del piano.

Noi abbiamo invece fatto il controllo per una sola retta.

Se chiedessimo ad un qualsiasi artigiano esperto di controllare se un piano è orizzontale, vedremmo che l’artigiano pone la livella sul piano, controlla che la bolla sia al centro, poi ruota la livella e controlla di nuovo che la bolla sia al centro. Se nei due casi la bolla è al centro, l’artigiano afferma che il piano è orizzontale. Afferma cioè che tutte le rette del piano sono orizzontali.

L’artigiano ha ragione. Perché?

L’artigiano sta sfruttando, forse inconsapevolmente, alcuni importanti teoremi di geometria dello spazio riguardanti la perpendicolarità tra due rette e la perpendicolarità tra una retta e un piano.

Ma quando due rette dello spazio che si intersecano in un punto sono perpendicolari?

Per rispondere a questa domanda dobbiamo innanzitutto sapere che, date due rette che si intersecano in un punto, esiste uno ed un solo piano che contiene entrambe le rette.

E quindi per dare la definizione di rette perpendicolari tra loro possiamo ricorrere alla definizione che viene data in geometria del piano:

Definizione

Due rette di un piano che si intersecano in un punto si dicono perpendicolari tra loro se i quattro angoli che essi formano sono tutti uguali. Questi angoli vengono detti retti.

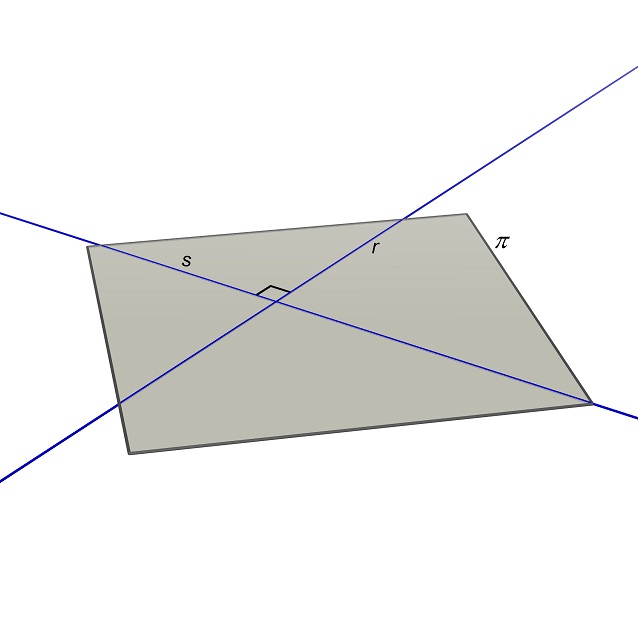
In effetti non è necessario controllare che tutti e quattro gli angoli siano retti. Basta controllare che uno di essi sia retto. Se lo è sono retti anche gli altri tre angoli. Lasciamo al lettore la dimostrazione di ciò.

Ora che conosciamo la definizione di rette tra loro perpendicolari possiamo tornare al nostro artigiano.

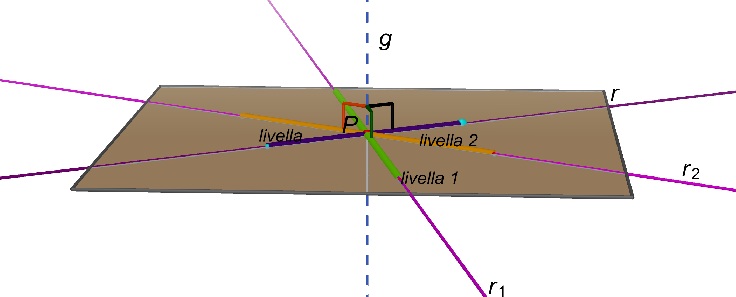
Ricordiamo che l’artigiano, dopo aver controllato che le rette r₁ e r₂ sono perpendicolari alla retta g, ha affermato che il piano è orizzontale; ha cioè affermato che tutte le rette del piano sono orizzontali.

Bene, si può dimostrare il seguente teorema.

Teorema (Proposizione 4 del libro XI degli Elementi di Euclide)

Siano dati una retta g un piano che si intersercano in un punto P.

Se la retta g è perpendicolare a due rette distinte r₁ e r₂ del piano passanti per P, allora la retta g è perpendicolare a qualsiasi retta r del piano passante per P.

Cliccando sulla figura si può ruotare la retta r sul piano passante per le rette r₁ e r_{2 .}

Da ciò possiamo dedurre che tutte le rette del piano passanti per P sono perpendicolari alla retta g e quindi sono orizzontali.

È utile la seguente definizione:

Definizione (Definizione 3 del libro XI degli Elementi di Euclide)

Una retta e un piano che si intersecano in un punto O si dicono perpendicolari se la retta è perpendicolare a tutte le rette del piano passanti per il punto O

E quindi il nostro teorema precedente può essere enunciato nel seguente modo:

Teorema

Siano dati una retta g un piano che si intersercano in un punto P.

Se la retta g è perpendicolare a due rette distinte r₁ e r₂ del piano passanti per P, allora la retta g è perpendicolare al piano.

Torniamo al nostro problema.

Abbiamo controllato che tutte le rette appartenenti al piano passanti per P sono perpendicolari alla retta g passante per P corrispondente alla gravità.

Ora dovremmo controllare che ogni altra retta del piano è orizzontale.

Consideriamone una. Chiamiamola s.

Cliccando sulla figura si può muovere il punto P’.

Consideriamo un suo punto P’ e consideriamo la retta g’ corrispondente alla forza di gravità applicata in P’. Dovremmo controllare che la retta s è perpendicolare alla retta g’.

Abbiamo che le due rette g e g’ passanti per P e P’ corrispondenti alla forza di gravità sono parallele.

Ci viene allora in aiuto un altro teorema della geometria dello spazio.

Teorema (Proposizione 8 del libro XI degli Elementi di Euclide)

Se un piano è perpendicolare ad una retta, allora è perpendicolare a qualsiasi retta parallela alla retta stessa.

Da questo teorema segue la retta s è perpendicolare a g’ e quindi è orizzontale.

Non è quindi necessario porre il centro della livella in un altro punto del piano.

Abbiamo quindi una risposta alla domanda che ci è stata posta.

RISPOSTA

Se la livella, posta su due rette non parallele del tavolo, ha in entrambi i casi la bolla al centro, allora il piano è orizzontale.

Non è quindi necessario fare altre prove.

Ciò deriva da alcuni teoremi di geometria dello spazio.