Domanda 3 a)

Consideriamo due punti distinti A e B. Consideriamo un piano π passante per essi.

Quante sono le circonferenze contenute nel piano π passanti per A e B?

Dove si trovano i centri di tali circonferenze?

Per rispondere alla domanda chiediamoci quali sono i punti del piano centri di tali circonferenze.

I centri di tali circonferenze devono essere ovviamente equidistanti dai punti A e B.

Dalla geometria del piano sappiamo che il luogo dei punti del piano equidistanti dai punti A e B è dato dalla retta asse del segmento AB.

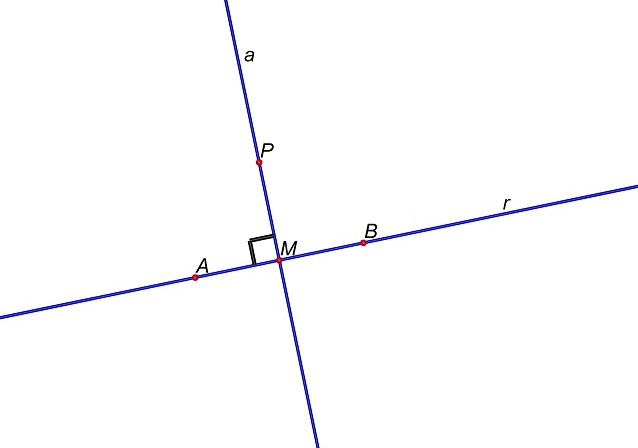
In altre parole i punti P del segmento AB sono tutti e soli i punti del piano equidistanti dai punti A e B.

Cliccando sulla figura si può muovere il punto P

Si consiglia vivamente di dimostrare quest’ultima affermazione.

Consideriamo ora la circonferenza del piano di centro P e passante per A.

Cliccando sulla figura si può muovere il punto P

Per ognuno degli infiniti punti P dell’asse del segmento AB abbiamo una circonferenza passante per A e B.

Abbiamo quindi la risposta alla nostra domanda:

Esistono infinite circonferenze passanti per A e B. I loro centri sono tutti e soli i punti della retta asse del segmento AB.

Domanda 3 b)

Consideriamo due punti distinti A e B.

Quante sono le sfere passanti per A e B?

Dove si trovano i centri di tali sfere?

Per rispondere alla domanda chiediamoci quali sono i punti centri di tali sfere.

I centri di tali sfere devono essere ovviamente equidistanti dai punti A e B.

Per determinare tutti questi punti usiamo quel che abbiamo visto nella risposta alla domanda precedente.

Consideriamo un punto Q qualsiasi dello spazio e consideriamo il piano π passante per A, B e Q.

Cliccando sulla figura si può muovere il punto Q

Sappiamo quali sono i punti del piano π equidistanti da A e B:

sono tutti i punti della retta asse del segmento AB sul piano π .

Cliccando sulla figura si può muovere il punto Q

Facendo variare il punto Q nello spazio e ripetendo ogni volta il ragionamento fatto, otteniamo altre rette assi del segmento AB.

Tutti i loro punti sono equidistanti da A e B.

Tutte le rette assi passano per il punto M medio di A e B e sono perpendicolari al segmento AB.

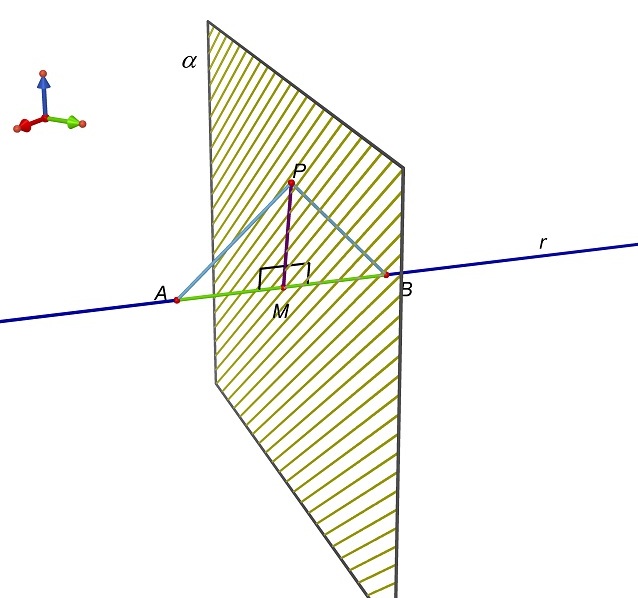
Sappiamo che tutti queste rette appartengono al piano α passante per M e perpendicolare alla retta passante per A e B.

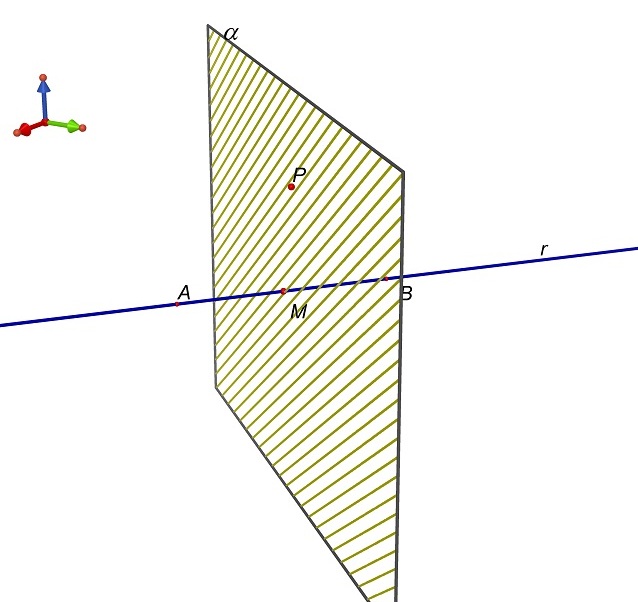
Chiamiamo il piano α, piano asse di A e B. Tutti i suoi punti sono equidistanti da A e B.

Ci chiediamo se esistano altri punti dello spazio che sono equidistanti da A e B.

Consideriamo un punto P che sia equidistante da A e B.

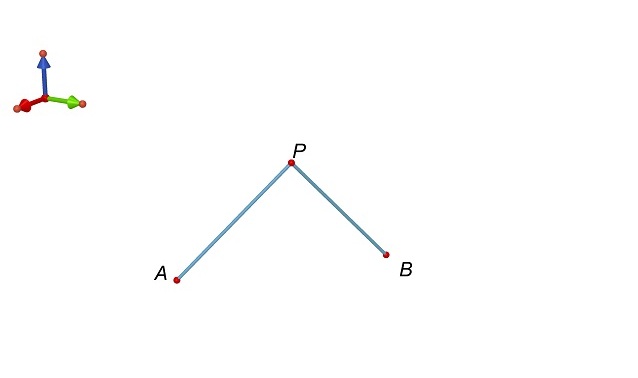
Vogliamo dimostrare che P appartiene al piano asse α.

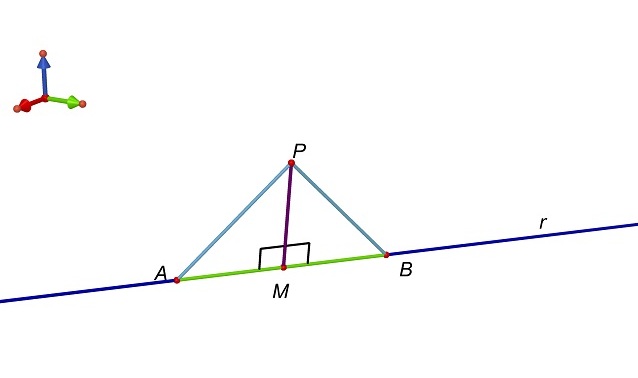
Per far ciò consideriamo i triangoli AMP e BMP.

I due triangoli hanno i tre lati a coppie uguali.

Quindi sono uguali. In particolare sono uguali gli angoli <AMP e <BMP. Essendo questi due angoli supplementari, essi sono retti.

Cliccando sulla figura si può muovere il punto P

Pertanto la retta passante per P e M, essendo perpendicolare alla retta passante per A e B, appartiene al piano asse α.

Cliccando sulla figura si può muovere il punto P

Abbiamo quindi dimostrato il seguente teorema:

Il luogo dei punti dello spazio equidistanti da due punti A e B distinti è dato dal piano asse del segmento AB.

Abbiamo anche risposto alla nostra domanda:

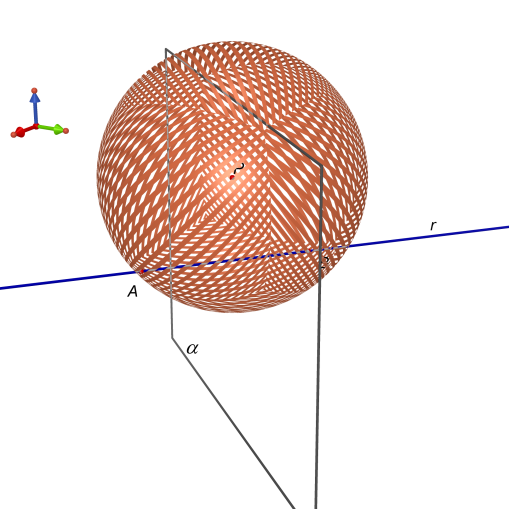
Esistono infinite sfere passanti per A e B. I loro centri sono tutti e soli i punti del piano asse del segmento AB.

Cliccando sulla figura si può muovere il punto P